直流电机稳压问题
背景与进展
在如下硬件设计中
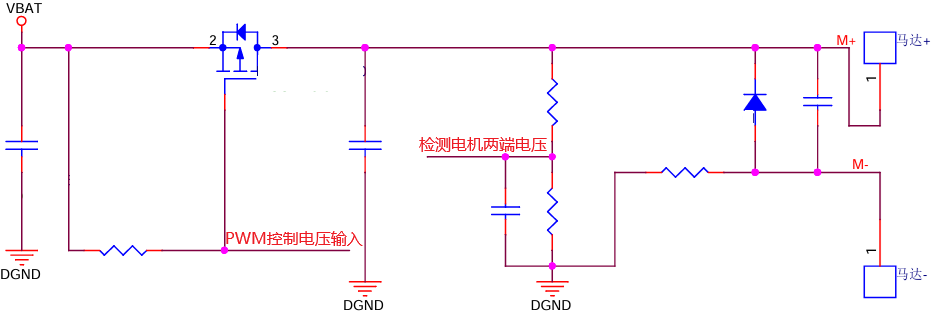
软件需通过ADC实时检测电机两端的输入电压,并以此调节PWM占空比,使电机电压保持稳定。主要技术难点如下:
ADC采样受PWM波形干扰
电机电压由PWM控制,其波形与PWM同步波动,导致ADC采集到的电压值跳动较大,与万用表测得的相对稳定值存在显著差异。PWM频率需权衡性能
提高PWM频率有助于ADC获取更稳定的采样值,但受限于MCU外设性能,实际频率通常设定在2KHz(最低要求)至4KHz或更高(性能较好的MCU)。尚未建立稳定的控制模型
尽管提高PWM频率对ADC检测有积极影响,但如何根据采样电压动态调节PWM占空比,以实现电压稳定控制,目前仍缺乏有效的数学模型。电压波动主要受电池供电状态、电机负载及内阻等因素影响,系统控制逻辑尚处于研究与试验阶段。
系统目标
这是一个典型的闭环电压调节问题,其简化系统框图如下
扰动 (电池电压、负载、内阻)
↓
[PWM占空比 D] → [电机 + 驱动电路] → [实际电机电压 V_actual]
↑ |
[ 控制器 ] ← [ADC采样 + 信号调理 → V_estimated]
↑
[设定值 V_target]根本目标:设计一个控制器,它能根据估算出的电机平均电压 V_estimated,动态、实时地调整PWM占空比 D,使得 V_estimated 在各种扰动(电池电压 V_bat 下降、负载变化、电机温升导致内阻 R_m 变化)下,都能快速、稳定地跟踪目标电压 V_target。
当前方案
理论基础
当前方案参照如下基本公式进行稳压控制:
Motor_PWM占空比 = (2 * (V_target / V_bat) - (V_measured / V_bat)) * 100即
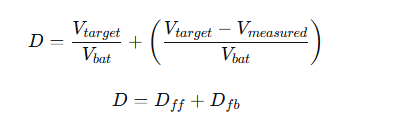
其中:
Dff=Vtarget/VbatDff: 这是前馈项。基于理想模型
所需电压 = 占空比 × 电池电压
直接计算出达到目标电压所需的理论占空比。它用于快速响应电池电压(V_bat)的变化和目标电压(V_target)的设定。
Dfb=(Vtarget−Vmeasured)/Vbat: 这是反馈项。它根据当前电压误差 (V_target - V_measured) 进行一个固定比例(比例系数为 1/Vbat)的修正。当实测电压低于目标时,此项为正,增加占空比;反之则减少。
现有方案的优点:
结构清晰:融合了前馈和反馈思想。
响应快速:前馈项能立刻跟随 V_bat 和 V_target 的变化。
计算简单:仅需一次除法和加减法,计算负荷极低。
现有方案的问题:
反馈环节过于简单:反馈项本质上是一个比例系数为变量(1/V_bat)的比例控制器(P-Controller)。
缺点1:存在稳态误差(静差):纯比例控制无法完全消除误差。当系统存在持续扰动(如电机内阻压降、电路损耗)时,V_measured 将永远无法精确等于 V_target,会存在一个固定的偏差。
缺点2:动态性能有限:比例系数 K_p = 1/V_bat 是随电池电压变化的,这可能不是最优的固定增益。系统在负载突变时可能会产生较大超调或恢复缓慢。
依赖高精度信号:公式直接使用 V_measured,如果ADC采样到的电压波动大(PWM纹波),会导致占空比 D 剧烈抖动,系统不稳定。
实际运用
按照基础公式设计的系统,电压偏离很大。
在公式的基础上根据不同目标电压进行调整,如下:(
// 2.0V
pwm_value = (10000 - mvol * 4) / (mvbat / 10);(这里对代码不作详解)
同时根据实时电压与电池电压的偏离程度动态地对PWM定时器的重载值(ARR值)进行补偿,如下:
if (arg1 > (mvol * 4))
{
pwm_value = (arg1 - mvol * 4) / (mvbat / 10);
if (mvol < arg2)
{
pwm_value = pwm_value + (arg2 - mvol) / 5;
}
//
if ((mode == 0) && (mvbat < 3650))
{
pwm_value += 10;
}
else if (mode == 1)
{
pwm_value += 10;
}
//
if (pwm_value > 200)
{
pwm_value = 200;
}
else if (pwm_value < 5)
{
pwm_value = 5;
}
}
else
{
pwm_value = 5;
}(这里对代码不作详解)
在经过不断测试与调整中,勉强实现了维持若干个目标电压的稳定(通过万能表实测验证)。
工程缺陷
为了弥补基础公式的缺陷,代码引入了大量经验性、条件性的补偿。
本质上这是一个由多个“IF-THEN”规则堆砌而成的专家系统,而非一个基于统一模型的控制系统。每个条件分支和补偿值都是在特定测试场景下“试出来”的补丁。
其核心问题在于:
高度脆弱与难维护:控制器行为严重依赖于 arg1, arg2, mode 等多个“魔法数字”和状态。任何硬件变更(如电机型号、采样电阻)、环境变化或新增工作模式,都可能需要重新调整所有数字,调试成本呈指数级增长。
逻辑耦合严重:补偿项层层嵌套,相互影响。调整一个参数可能意外破坏另一个工况下的性能。
可解释性差:很难从这一堆条件语句中理解“系统为什么要这样调整”,这使得后续工程师难以接手和优化。
控制性能天花板低:它只能在已测试过的、有限的几个目标电压点上“勉强稳定”。对于目标电压的连续变化,或者未测试过的负载扰动,其性能无法预测和保证。
浪费大量调试时间:达到“勉强稳定”的状态,已经耗费了巨大的测试和凑参数时间。
优化思路
当前的代码是解决复杂控制问题时常见的“第一步”——通过直觉和经验让系统先跑起来,不具备可维护性和扩展性(体现为各种arg和补偿值)。
需要一个简洁的数学模型(前馈)和一个鲁棒的控制算法(PID) ,使系统从“勉强实现”变为“可靠稳定”。
在现有前馈-反馈的优秀框架基础上,将其中简单的比例反馈升级为完整的PID反馈,并加入必要的信号处理。
优化后的控制律:

具体实施步骤:
步骤1:信号预处理(必须做)
对 V_measured (即 Motor_AD) 进行低通滤波,采用 一阶低通数字滤波器(LPF) 或 移动平均滤波器。
// 一阶低通数字滤波器示例 (系数alpha = 0.1 ~ 0.3)
float alpha = 0.2; // 时间常数,越小越平滑,滞后越大
V_filtered = alpha * V_measured + (1 - alpha) * V_filtered_prev;同理,对 V_bat 的测量值也可以进行轻度滤波,避免其跳变引起前馈项突变。
步骤2:升级反馈控制器为增量式PID
步骤3:参数整定与调试